ขั้นคิดคำนวณแบบควอนตัม

เมื่อหนึ่งปีเต็มที่แล้วถูกชักชวนจากจิรวัฒน์ ตั้งปณิธานนท์ (Center for Quantum Technologies, สิงคโปร์) ให้ไปช่วยเขียนหนังสือให้ความรู้เกี่ยวกับคอมพิวเตอร์เชิงควอนตัม ด้วยความช่วยเหลือตรวจแก้จากบรรณาธิการและผู้ร่วมชะตากรรมเขียนคนอื่นๆทำให้สำเร็จออกมาเป็นหนังสือ(ฟรี) รูป รส กลิ่น เสียง สัมผัส ไอทีควอนตัม (๓): “คอมพิวเตอร์เชิงควอนตัม” จนได้ แต่ส่วนที่มีคณิตศาสตร์ที่เกินกว่าการนับเลขถูกตัดออกหมดก็เลยอยากจะลงต้นฉบับที่มีคณิตศาสตร์ไว้ ณ ที่นี้เพื่อความเข้าใจคอมพิวเตอร์เชิงควอนตัมที่แม่นยำและลึกซึ้งขึ้นครับ (ขอขอบคุณปัณฑิตา ผลิตผลการพิมพ์ ที่อ่านและวิจารณ์ดราฟท์แรกอย่างละเอียดจนกลายมาเป็นต้นฉบับนี้ได้ แต่ข้อผิดพลาดใดๆหรือภาษาที่ไม่สละสลวยเป็นความรับผิดชอบของผมเอง)

---

อัลกอริธึมนั้นสำคัญไฉน

นี่คือหน้าตาของเมืองเคอนิกสแบร์ก (Königsberg) ในศตวรรษที่ 18 ที่แม่น้ำ Pregel ไหลผ่านตัดแยกตัวเมืองเป็นสี่ผืนดินที่เชื่อมกันด้วยสะพานเจ็ดสะพาน (ก่อนจะเหลือแค่ห้าจากการทิ้งระเบิดสมัยสงครามโลกครั้งที่สอง) ชาวเมืองเคอนิกสแบร์กมักจะใช้เวลาบ่ายวันอาทิตย์เดินชมเมืองอันสวยงามของพวกเขา จนมีคนนึกสนุกตั้งปัญหาขึ้นมาว่าเป็นไปได้ไหมที่จะเดินข้ามสะพานครบทั้งเจ็ดสะพานโดยไม่ข้ามสะพานใดสะพานหนึ่งมากกว่าหนึ่งครั้ง?

อีกปัญหาที่มีความคล้ายกันมากมาจากเกมที่วิลเลียม โรวัน แฮมิลตัน (William Rowan Hamilton) ชาวไอริชคิดขึ้นในปี 1857 ชื่อว่าเกมไอโคเซียน (Icosian) เป้าหมายของเกมคือการหาเส้นทางเดินบนขอบ (ที่เป็นเส้นหนึ่งมิติ ไม่ใช่หน้า) ของรูปเหลี่ยม 12 หน้า (dodecahedron) ที่ผ่านทุกมุมแต่ไม่ผ่านมุมใดมุมหนึ่งมากกว่าหนึ่งครั้ง

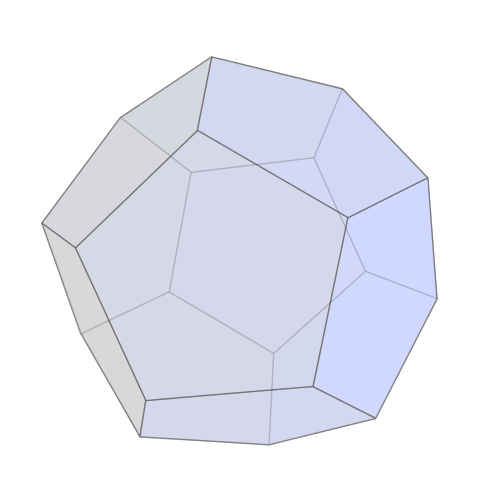
ในทางคณิตศาสตร์แล้ว ทั้งสองปัญหาคือปัญหาเกี่ยวกับการเดินบนเน็ตเวิร์คซึ่งเป็นโครงสร้างที่ประกอบด้วยเส้นเชื่อม (edge) และโหนด (หรือจุดยอด vertex) เกมไอโคเซียนถามหาเส้นทางเดินบนเน็ตเวิร์คที่ผ่านทุกๆโหนดแต่ไม่ผ่านโหนดใดโหนดหนึ่งมากกว่าหนึ่งครั้ง ในขณะที่ปัญหาสะพานทั้งเจ็ดของเคอนิกสแบร์กถามหาเส้นทางเดินบนเน็ตเวิร์คที่ผ่านทุกๆเส้นเชื่อมแต่ไม่ผ่านเส้นเชื่อมใดเส้นเชื่อมหนึ่งมากกว่าหนึ่งครั้ง

เลออนฮาร์ด ออยเลอร์ (Leonhard Euler) ชาวสวิตเซอร์แลนด์ที่ช่วงนั้นทำงานอยู่ที่เซนต์ ปีเตอร์สเบอร์ก สังเกตว่าปัญหาสะพานทั้งเจ็ดของเคอนิกสแบร์กจะมีคำตอบก็ต่อเมื่อไม่มีโหนดที่มีเส้นออกจากโหนดเป็นจำนวนคี่ หรือถ้ามีก็มีแค่สองโหนด เพราะการผ่านโหนดใดโหนดหนึ่งโดยไม่เดินซ้ำเส้นทางเดิมจะต้องมีทางเข้าทางหนึ่งกับทางออกทางหนึ่ง แต่โหนดเริ่มต้นไม่ต้องมีทางเข้าและโหนดสุดท้ายไม่ต้องมีทางออก คำตอบของออยเลอร์ลึกซึ้งที่ว่ามันไม่ใช่คำตอบของปัญหาสะพานทั้งเจ็ดของเคอนิกสแบร์กปัญหาเดียวแต่เป็นคำตอบของการเดินโดยไม่ซ้ำเส้นทางเดิมบนทุกๆเน็ตเวิร์ค และมันยังบอกขั้นตอนการหาคำตอบหรืออัลกอริธึม (algorithm) ที่มีประสิทธิภาพสำหรับทุกๆเน็ตเวิร์คโดยการนับจำนวนเส้นเชื่อมที่ออกจากโหนดแต่ละโหนดเท่านั้น

ทว่าจนถึงทุกวันนี้ยังไม่มีใครรู้อัลกอริธึมเร็วๆสำหรับเกมไอโคเซียนที่ใช้ได้กับทุกๆเน็ตเวิร์ค ซึ่งน่าคิดเพราะเกมไอโคเซียนต่างกับปัญหาสะพานทั้งเจ็ดของเคอนิกสแบร์กเพียงแค่เปลี่ยนเส้นเชื่อมเป็นโหนดเท่านั้นเอง อัลกอริธึมที่ใช้ได้กับทั้งสองปัญหาก็คือลองเดินมันโง่ๆทุกเส้นทางบนเน็ตเวิร์คแล้วดูว่ามีเส้นทางที่เป็นคำตอบไหม แต่วิธีนี้อาจจะต้องใช้เวลาเป็นทวีคูณ (exponential) ของขนาดของเน็ตเวิร์ค จำนวนที่เป็นทวีคูณนี่ใหญ่ขนาดกันนะ?

ในนิทานเรื่องหนึ่ง พระราชาเรียกผู้ที่คิดเกมหมากรุกได้เป็นคนแรกมาเข้าเฝ้าหวังจะให้รางวัลตอบแทนอย่างยิ่งใหญ่สมกับผลงานของเขา คนผู้นั้นก็ขอรางวัลเป็นข้าวสารหนึ่งเม็ดในช่องแรกของกระดานหมากรุก สองเม็ดในช่องที่สอง สี่เม็ดในช่องที่สาม… เพิ่มขึ้นที่ละสองเท่าตัวๆจนเต็ม 64 ช่องของกระดานหมากรุก พระราชาก็รับปากถึงแม้ในใจจะคิดว่าข้าวสารแค่นี้จะมีค่าสักเท่าไรเชียว จนกระทั่งคนรับใช้กะปริมาณข้าวสารที่ต้องให้

• 1,000,000 เม็ดในช่องที่ 20
• 1,000,000,000,000 เม็ดในช่องที่ 40
• 18,000,000,000,000,000,000 เม็ดในช่องสุดท้ายซึ่งถ้าตีเป็นน้ำหนักก็จะได้ประมาณ 460,000,000 ตัน!

บางเวอร์ชันของเรื่องเล่านี้จบลงที่พระราชาสั่งประหารคนผู้นั้นเมื่อรู้ตัวว่าโดนหลอกเข้าให้แล้ว บทเรียนหนึ่งของเรื่องนี้ก็คืออย่าไปกวนตีนคนที่มีอำนาจมากนัก แต่อีกบทเรียนที่สำคัญกว่าก็คือจำนวนที่โตแบบทวีคูณนั้นอาจจะโตเกินจินตนาการของเราได้ ถึงปัญหาจะไม่ใหญ่มาก แต่ถ้ามีแต่อัลกอริธึมที่ต้องใช้เวลาเป็นทวีคูณ ถึงจะใช้ซูเปอร์คอมพิวเตอร์ที่ทำการคำนวณได้กว่า 10 ยกกำลัง 15 ขึ้นตอนในหนึ่งวินาทีก็ยังอาจต้องใช้เวลาเกินอายุปัจจุบันของเอกภพ (13.7 พันล้านปี) ในขณะที่ดวงอาทิตย์อยู่ได้อีกแค่ประมาณห้าพันล้านปี อัลกอริธึมที่ช้าจึงไม่ใช่แค่ไม่ทันใจ แต่อาจจะไม่ทันโลกแตกด้วยซ้ำ! ปัญหาที่ต้องใช้เวลาเป็นทวีคูณในการแก้ถือเป็นปัญหาที่ยาก

บัตรเครดิต, เสียงดนตรี, และคอมพิวเตอร์ควอนตัม

ไอเดียของคอมพิวเตอร์ที่อาศัยพฤติกรรมเชิงควอนตัมของสสารในการคำนวณมีมาตั้งแต่ปี 1980 แล้วแต่ในตอนนั้นยังไม่ชัดเจนว่าคอมพิวเตอร์ควอนตัมจะแก้ปัญหายากๆได้เร็วกว่าคอมพิวเตอร์ธรรมดาขนาดไหน จุดเปลี่ยนที่ทำให้คนหันมาสนใจคอมพิวเตอร์ควอนตัมในวงกว้างมาจากวงการที่แทบจะไม่เกี่ยวข้องกับฟิสิกส์เลย: วงการรหัสลับ

การส่งข้อความลับจะต้องมีกุญแจเข้ารหัส (encrypt) และกุญแจถอดรหัส (decrypt) รหัสลับก่อนสงครามโลกครั้งที่สองมักใช้กุญแจเดียวกันทั้งในการเข้าและถอดรหัส จึงถูกเรียกว่ากุญแจแบบสมมาตร (symmetric key) รหัสแบบนี้สามารถให้ความปลอดภัยอย่างสมบูรณ์แบบได้ในทางทฤษฎีเช่น one-time pad ที่มีกุญแจเป็นข้อความสุ่มมั่วๆเอามาใช้แปลงข้อความจริง ถ้ารู้ข้อความสุ่มนั้นก็จะกู้ข้อความจริงกลับมาได้ แต่กุญแจต้องใช้แล้วทิ้ง ห้ามใช้ซ้ำกัน ตามชื่อว่า one-time (การที่โปรเจ็กต์ VENONA ของ NSA สหรัฐอเมริกาจับตัวสายลับโซเวียตในช่วงสงครามโลกครั้งที่สองได้ก็เชื่อกันว่ามาจากการใช้กุญแจซ้ำของโซเวียตที่มีเหตุจากการเร่งการผลิตกุญแจลับเพราะการบุกของเยอรมัน) ยิ่งข้อความลับยาวกุญแจก็ยิ่งต้องใหญ่ นอกจากนี้การที่ทั้งผู้ส่งและผู้รับจะต้องมีกุญแจเดียวกันก็แปลว่าจะต้องมีการส่งกุญแจกันไปมา ถ้าถูกดักตีหัวขโมยกุญแจก็เสร็จ

ในปัจจุบันรหัสลับส่วนใหญ่ใช้กุญแจคนละดอกในการเข้าและถอดรหัส โดยกุญแจเข้ารหัสเป็นกุญแจสาธารณะ (public key) ที่ใครๆก็รู้ได้ ระบบแบบนี้ไม่มีทางปลอดภัยอย่างสมบูรณ์แบบเพราะข้อมูลของกุญแจถอดรหัสก็อยู่ในกุญแจเข้ารหัส (ทั้งสองกุญแจมีความสัมพันธ์กันเพราะกุญแจถอดรหัสต้องแก้สิ่งที่กุญแจเข้ารหัสทำ) การค้นพบครั้งสำคัญในวงการรหัสลับคือการใช้ปัญหาการแยกตัวประกอบที่เชื่อว่าไม่มีอัลกอริธึมใดๆในปัจจุบันแก้ได้เร็วพอมาป้องกันการกู้กุญแจถอดรหัสจากกุญแจเข้ารหัส การเข้ารหัสนี้เรียกว่าการเข้ารหัสแบบ RSA ¹ และเป็นระบบการเข้ารหัสที่ใช้กันแพร่หลายในการเข้าเวบอย่างปลอดภัย (https), การป้องกันพาสเวิร์ด, หรือบัตรเครดิต ทุกครั้งที่เราซื้อของออนไลน์ ความปลอดภัยของเราขึ้นอยู่กับ RSA

ถ้าดูนาฬิกาเป็นก็จะเข้าใจไอเดียของ RSA ได้ สังเกตว่าในการบวก-ลบเวลา เราจะไม่พูดว่า “10 ชั่วโมงหลัง 20 นาฬิกาคือ 30 นาฬิกา” แต่เราจะเริ่มนับส่วนที่เกิน 24 ใหม่ นอกจากบวก-ลบแล้วการคูณหรือการยกกำลังในระบบเลขคณิตแบบนี้ก็เป็นสิ่งที่ทำได้เพราะการคูณคือการบวกซ้ำๆกันและการยกกำลังคือการคูณซ้ำๆกัน ซึ่งคนส่วนใหญ่คงจะไม่เคยทำ แต่ถ้าลองทำดูจะพบสิ่งหนึ่งที่น่าสนใจคือการคูณเลขด้วยตัวมันเองซ้ำๆจะทำให้ย้อนกลับมายังเลขตั้งต้นได้ ตารางด้านล่างเป็นผลคูณ 2 ด้วยตัวมันเองถ้ามี 15 ชั่วโมงในหนึ่งวัน

กำลัง $x$	1	2	3	4	5	6	7
ค่าของ $2^x$	2	4	8	1	2	4	8

การเข้ารหัสแบบ RSA แปลงข้อความให้เป็นจำนวนเต็มก่อน เรียกจำนวนนี้ว่า $m$ (message) กุญแจสาธารณะคือจำนวนของ“ชั่วโมง” $N$ และตัวเลข $x$ ที่ทำให้ผู้เข้ารหัสสามารถคำนวณ $m$ ยกกำลัง $x$ ในเลขคณิตแบบนาฬิกาได้ เมื่อถึงมือผู้รับรหัส มีกุญแจลับ $y$ ที่บอกว่าจะต้องยกกำลังต่ออีกเท่าไรจึงจะได้ข้อความ $m$ กลับมา การจะรู้ $y$ ได้จะต้องแยกตัวประกอบของ $N$ ซึ่งเป็นส่วนหนึ่งของกุญแจสาธารณะที่ใครๆก็มี แต่ปัญหาก็คือทุกๆอัลกอริธึมการแยกตัวประกอบที่มีในปัจจุบันต้องใช้เวลาเป็นทวีคูณ การจะถอดรหัส RSA ที่ $N$ เป็นเลขหลายร้อยหลักอาจจะต้องใช้เวลาเป็นล้านปี

แต่ถ้ามีคอมพิวเตอร์ควอนตัม การแยกตัวประกอบเลขหลายร้อยหลักจะใช้เวลาเพียงไม่กี่วินาที! ² สิ่งที่ต่างก็คือคอมพิวเตอร์ควอนตัมมีอัลกอริธึมควอนตัมที่สามารถหาทางลัดในการแก้บางปัญหาได้ การทำงานของอัลกอริธึมควอนตัมแยกตัวประกอบค่อนข้างซับซ้อนแต่หัวใจของมันมาจากการทำงานร่วมกันของการยกกำลังในเลขคณิตนาฬิกากับการแปลงฟูเรียร์ (Fourier transform) การแปลงฟูเรียร์เป็นการแตกคลื่นเป็นผลรวมของหลายๆคลื่นที่มีความถี่เฉพาะตัว ไม่ต่างกับการแยกเสียงดนตรีเป็นโน๊ตความถี่ต่างๆ ทำให้สามารถขับหรือลดเสียงของเครื่องดนตรีแต่ละชนิดแยกกันได้ หน้าที่ของการแปลงฟูเรียร์ในอัลกอริธึมควอนตัมคือการหาคาบ (ส่วนกลับของความถี่) ของการยกกำลังในเลขคณิตนาฬิกา เมื่อรู้คาบ — จำนวนครั้งที่ต้องคูณเพื่อให้ได้ค่าเดิมกลับมา — ก็จะทำให้แยกตัวประกอบและรู้ $y$ ได้ จึงทำลายรหัสลับ RSA ได้

บางปัญหาที่ยากสำหรับคอมพิวเตอร์ธรรมดาเป็นปัญหาที่ง่ายสำหรับคอมพิวเตอร์ควอนตัม นี่เป็นการค้นพบของ ปีเตอร์ ชอร์ (Peter Shor) ชาวอเมริกันในปี 1994 ที่สั่นสะเทือนวงการการถอดรหัสลับและฟิสิกส์ ปัจจุบันยังไม่มีคอมพิวเตอร์ควอนตัมขนาดใหญ่พอที่จะทำแบบนี้ได้ อินส์บรุค (Innsbruck) จับมือกับ MIT เพิ่งจะตีพิมพ์การแยกตัวประกอบ 15 ออกเป็น 3x5 ได้สำเร็จด้วยคอมพิวเตอร์ควอนตัมจิ๋ว 5 อะตอมเมื่อปีที่แล้ว ³ แต่ก็ไม่ต้องห่วงว่าถ้าทำสำเร็จโลกนี้จะไม่มีความลับอีกต่อไปเพราะนักวิทยาศาสตร์ได้เตรียมรหัสลับต้านทานอัลกอริธึมควอนตัมไว้เรียบร้อยแล้ว (post-quantum cryptography)

เรขาคณิตของอัลกอริธึมควอนตัม

ความเข้าใจผิดที่ได้ยินกันแพร่หลายมากที่สุดเกี่ยวกับคอมพิวเตอร์ควอนตัมคือคอมพิวเตอร์ควอนตัมเหมือนกับคอมพิวเตอร์ธรรมดาที่ประมวลผลแบบคู่ขนาน แก้ปัญหาโดยการเช็คคำตอบทุกคำตอบที่เป็นไปได้พร้อมๆกัน ซึ่งถ้าทำได้จริงก็จะมหัศจรรย์มาก ไม่ว่าปัญหาใดๆ อัลกอริธึมควอนตัมที่ลองทุกคำตอบก็จะแก้ได้ในหนึ่งขั้นตอนเท่านั้น แต่ความจริงไม่ง่ายแบบนั้น ซึ่งก็อาจจะเป็นเรื่องดีเพราะการเข้ารหัสลับที่ต้านทานอัลกอริธึมควอนตัมก็ต้องอาศัยปัญหาที่ยากสำหรับทั้งอัลกอริธึมธรรมดาและอัลกอริธึมควอนตัม ตัวอย่างที่ดีเยี่ยมในการแสดงให้เห็นการความแตกต่างของการทำงานของอัลกอริธึมธรรมดากับอัลกอริธึมควอนตัมจึงเป็นอัลกอริธึมควอนตัมในการเช็คคำตอบที่ลอฟ โกรเวอร์ (Lov Grover) ชาวอเมริกัน-อินเดีย คิดขึ้นมาในปี 1996 หลังจากชอร์ 2 ปี

การจะเข้าใจการทำงานของอัลกอริธึมนี้จะต้องรู้พื้นฐานของทฤษฎีควอนตัมเสียก่อนทฤษฎีควอนตัมรวมคณิตศาสตร์ของความน่าจะเป็นกับเรขาคณิต แต่เป็นเรขาคณิตที่มีแต่ทิศทาง ไม่มีขนาด (สำหรับคนที่รู้จักเวกเตอร์ จึงไม่ใช่เรขาคณิตของเวกเตอร์เสียทีเดียวเพราะเวกเตอร์มีทั้งขนาดและทิศทาง) ในเรขาคณิตแบบนี้ เหนือกับใต้ถือว่าเป็นทิศเดียวกันเพราะการเดินไปทางเหนือก็คือการเดินไปทางใต้ด้วยระยะทางติดลบ พูดอีกอย่างก็คือมุม 180 องศากลายเป็น 0 องศา (แทนที่ 360 องศาจะเป็น 0 องศา) แต่ความใกล้กันของสองทิศทางก็ยังวัดได้ด้วยมุมที่ไม่เกิน 90 องศา สิ่งที่สำคัญคือยังมีทิศทางที่ตั้งฉากกัน (ทำมุม 90 องศา) นิยามของมิติจึงเหมือนกับในเรขาคณิตปกติ คือจำนวนที่มากที่สุดของทิศทางที่ตั้งฉากกัน เหมือนที่ 3 มิติมีความกว้าง ความยาว และความสูง ⁴

ระบบฟิสิกส์ไม่ว่าจะเป็นอะตอม ไอออน ช่องว่างในเพชร หรือวงจรไฟฟ้ายิ่งยวด ที่จะได้เจอในบทถัดๆไปของหนังสือเล่มนี้จะมีสถานะควอนตัม (quantum state) ของมันเองถ้าได้รับการป้องกันอย่างดีพอจากสิ่งรบกวนภายนอกไม่ว่าจะเป็นสนามแม่เหล็กไฟฟ้าหรือความร้อน ซึ่งตามทฤษฎีควอนตัมแล้ว ทิศทางเป็นตัวแทนเชิงคณิตศาสตร์ของสถานะควอนตัม ทิศทางนี้ไม่ใช่ทิศทางจริงๆในทางภูมิศาสตร์ แต่เป็นทิศทางในจำนวนมิติที่ถูกกำหนดโดยฟิสิกส์ของระบบนั้นๆ เช่นสถานะควอนตัมของสปินของอิเล็กตรอนถูกแทนด้วยทิศทางในสองมิติ

การวัดในทฤษฎีควอนตัมคือการถามระบบฟิสิกส์ว่าสถานะควอนตัมของเธอชี้ไปทางนี้หรือเปล่า? ถ้าทิศที่ถามขนานกับทิศที่มันชี้พอดีก็จะได้คำตอบว่า “ใช่” เสมอ ถ้าทิศที่ถามตั้งฉากกับทิศที่ชี้ก็จะได้คำตอบว่า “ใม่” เสมอ แต่จะเกิดอะไรขึ้นถ้าทิศที่ถามไม่ขนานหรือตั้งฉากเสียทีเดียวล่ะ? ทฤษฎีควอนตัมกำหนดว่าความน่าจะเป็นที่จะได้คำตอบ “ใช่” มีค่าเป็นกำลังสองของโคไซน์ของมุมระหว่างสองทิศนั้น

องศา $\theta$	0	30	45	60	90	120	135	150	180
ความน่าจะเป็น $\cos^2\theta$	1	3/4	1/2	1/4	0	1/4	1/2	3/4	1

สมมติว่าปัญหาหนึ่งมีคำตอบที่เป็นไปได้ 4 คำตอบ ปกติแล้วจะต้องเช็คคำตอบทีละคำตอบ จึงเป็นไปได้ว่าจะต้องเช็คถึง 4 ครั้งกว่าจะได้คำตอบที่ถูกต้อง สำหรับคอมพิวเตอร์ควอนตัม 4 คำตอบนี้แทนด้วย 4 ทิศทางที่ตั้งฉากกัน (จึงมี 4 มิติ) การเช็คคำตอบด้วยการวัดก็ไม่ช่วยอะไรเช่นกัน แต่คอมพิวเตอร์ควอนตัมสามารถเช็คคำตอบโดยปราศจากการวัดได้โดยการเก็บคำตอบ “ใช่” หรือ “ไม่ใช่” ไว้กับตัวมันเอง ซึ่งถ้าเราไม่ไปวัดก็จะไม่รู้ ดูเป็นความสามารถที่ไร้ประโยชน์สิ้นดี แต่ทริคของอัลกอริธึมควอนตัมคือการแปลงการเช็คคำตอบแบบหลังไปเป็นการพลิกสถานะควอนตัมที่ขนานกับทิศของคำตอบ ถ้าคำตอบอยู่ในทิศเหนือ-ใต้ (อย่าลืมว่าเป็นทิศเดียวกันในเรขาคณิตแบบควอนตัม) แล้วสถานะควอนตัมชี้ไปทางเหนือ การเช็คคำตอบก็จะพลิกมันมาทางทิศใต้ สถานะควอนตัมที่ชี้ไปทางใต้ก็จะถูกพลิกไปยังทิศเหนือ และปล่อยทิศทางที่ตั้งฉากกับคำตอบไว้คงเดิม ทริคนี้จึงไม่มีผลต่อความน่าจะเป็นของผลการวัดแต่อย่างใด แต่มันทำให้อัลกอริธึมควอนตัมหาหนึ่งในสี่คำตอบที่ถูกต้องเจอจากการเช็ค (พลิก) เพียงหนึ่งครั้งเท่านั้น! เริ่มต้นด้วยทิศที่มีโอกาสได้คำตอบทุกคำตอบเท่าๆกันหมดคือ 1/4 ทิศนี้ทำมุม 60 องศากับคำตอบ s (solution) เพราะว่าโคไซน์กำลังสองของ 60 องศาเท่ากับ 1/4

จากนั้นก็เช็คคำตอบเพื่อพลิกมัน

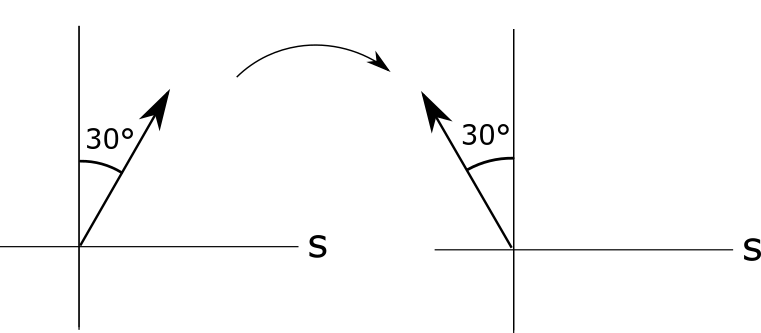
แล้วก็พลิกอีกครั้งผ่านทิศตั้งต้นก็จะได้คำตอบที่ถูกต้องด้วยความน่าจะเป็น 100%

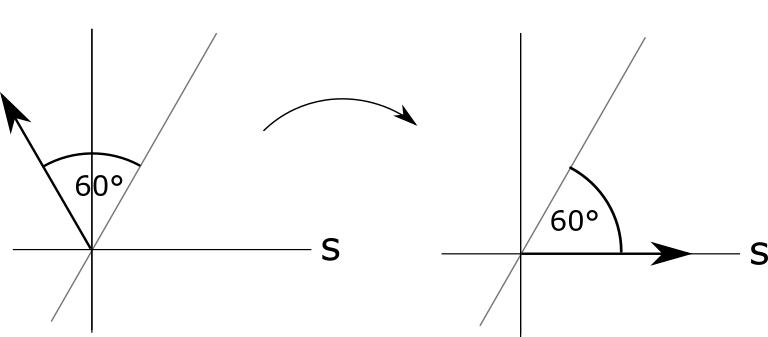
เมื่อคำตอบที่เป็นไปได้มีจำนวนเยอะขึ้น ทิศทางตั้งต้นก็จะอยู่ห่างจากทิศของคำตอบมากขึ้น การพลิกสองสเต็ป (จากการเช็คคำตอบ ตามด้วยการพลิกผ่านทิศตั้งต้น) แต่ละครั้งจะทำให้ขยับเข้าใกล้คำตอบมากขึ้นเรื่อยๆ หากทำการคำนวณก็จะประมาณได้ว่าจำนวนครั้งที่อัลกอริธึมนี้ต้องเช็คคำตอบคือรากที่สองของจำนวนคำตอบที่เป็นไปได้ ⁵ ถ้าคอมพิวเตอร์ธรรมดาต้องเช็คคำตอบหนึ่งล้านครั้ง คอมพิวเตอร์ควอนตัมก็จำเป็นต้องเช็คเพียงแค่หนึ่งพันครั้ง ไม่ได้เร็วขึ้นแบบทวีคูณเหมือนอัลกอริธึมแยกตัวประกอบของชอร์แต่ก็ช่วยได้เยอะ

ในมุมมองหนึ่ง สิ่งที่อัลกอริธึมควอนตัมทำจึงเป็นเพียงการขยับลูกศรไปมา ซึ่งพูดเหมือนง่ายแต่เป็นความท้าทายมาก ถ้าอยากรู้ว่าการควบคุมสถานะควอนตัมนั้นทำกันในแลบได้อย่างไรก็สามารถอ่านบทความที่เขียนและเรียบเรียงโดยนักศึกษาและนักวิทยาศาสตร์ไทยท่านอื่นๆ ได้ใน รูป รส กลิ่น เสียง สัมผัส ไอทีควอนตัม (๓): “คอมพิวเตอร์เชิงควอนตัม” ครับ

#อ้างอิง

• Cristopher Moore และ Stephan Mertens, “Quantum Computation” ใน The Nature of Computation, Oxford University Press (2011).

• Scott Aaronson, “Crypto” ใน Quantum Computing Since Democritus, Cambridge University Press (2013).

1. มาจากตัวอักษรแรกของชื่อผู้ค้นพบ Ron Rivest, Adi Shamir, และ Leonard Adleman ↩

2. ถ้าสมมติว่าคอมพิวเตอร์ควอนตัมมีความเร็ว CPU พอๆกับของคอมพิวเตอร์ปัจจุบัน ↩

3. Thomas Monz et al., “Realization of a scalable Shor algorithm” Science 351 1068 (2016). ↩

4. สำหรับผู้รู้ทฤษฎีควอนตัม ที่พูดไปไม่ใช่ความจริงทั้งหมดเพราะมุมนี้สามารถเป็นจำนวนเชิงซ้อนได้! แต่ทุกมุมในบทความนี้เป็นจำนวนจริง ↩

5. จริงๆคือ π/4 คูณรากที่สองของจำนวนคำตอบที่เป็นไปได้ ↩